I found myself browsing through Project Euler Today during my free time. After reading a couple of problems I payed special attention to Problem #12.
The problem goes like this:
The sequence of triangle numbers is generated by adding the natural numbers. So the 7th triangle number would be 1 + 2 + 3 + 4 + 5 + 6 + 7
= 28.The first ten terms would be: 1, 3, 6, 10, 15, 21, 28, 36, 45, 55, …
Let us list the factors of the first seven triangle numbers:
1: 1
3: 1,3
6: 1,2,3,6
10: 1,2,5,10
15: 1,3,5,15
21: 1,3,7,21
28: 1,2,4,7,14,28
We can see that 28 is the first triangle number to have over five divisors.
What is the value of the first triangle number to have over five hundred divisors?
The Solution
Getting the answer to this problem is fairly simple even though the obvious might not be the best way to go. Let’s see what can we learn from this.
Brute force!
Brute forcing your way through this problem is a possible solution, though it might take a long wait.
for( int i = 1; true; ++i )
{
int triangle = 0;
// Obtaining the triangle number
//
for( int j = 1; j <= i; ++j ) triangle += j;
int factors = 0;
// Counting the factors
//
for( int k = 1; k <= triangle; ++k )
{
if( triangle % k == 0 ) ++factors;
}
// If factors are bigger than 499 then exit
//
if( factors > 499 )
{
std::cout << "Triangle number: " << triangle << " factors: " << factors << std::endl;
break;
}
}
Results
Triangle number: 76576500
Time: 974.812segs ~ 16mins
Even though this is not the optimal solution for obvious reasons, it's a good way of proving yourself that you understood the problem and that you know how to get to the answer.
When solving problems like this, I tend to write the brute force version of the solution first. In addition, I use small test cases just to prove I'm on the right track; and then optimize in order to solve the problem efficiently.
Optimizing: Triangle Numbers
First let us dig into triangular or triangle numbers. According to the problem description, triangle numbers come from a sequence. If we use the sequence definition in order to get the triangle numbers, we can remove one of the bottlenecks of our solution.
Let us start by saying that triangle numbers are the additive analog of factorial numbers. Thus the sequence definition is:

This article goes into depth about demonstrating how T(n) = n ( n + 1) / 2
If we modify our code accordingly we must end up with something like
this:
for( int i = 1; true; ++i )
{
// Obtaining the triangle number
//
int triangle = i * ( i + 1 ) / 2;
int factors = 0;
// Counting the factors
//
for( int k = 1; k <= triangle; ++k )
{
if( triangle % k == 0 ) ++factors;
}
// If factors are bigger than 499 then exit
//
if( factors > 499 )
{
std::cout << "Triangle number: " << triangle << " factors: " << factors << std::endl;
break;
}
}
It’s worth mentioning that addition is a fairly fast operation; however, calculating the triangle number is not what is needed for a major performance overhaul in our original solution. Eliminating the loop to calculate the triangle number is a good improvement in terms of readability rather than improving the time of execution of our solution.
Results
Triangle number: 76576500
Time: 951.555segs ~ 15mins
This update its not worthless, but its not great either. Regardless of the technicalities of it, learning in depth about triangle numbers is a good addition (no pun intended ;) to our knowledge base and may help to clarify further math/programming problems.
Triangle Numbers: Alternate Methods
Division is a costly operation. Purists avoid using it whenever possible. We could change our code to avoid division with little effort.
int triangleNumber( int n )
{
int data = 0;
int next = 1;
while( n > 0 )
{
data = data + next;
next++;
n--;
}
return data;
}
I’ll let you guys decide on which is the most suitable solution for your standards.
Optimizing: Integer Factorization
Now people tend to interpret Integer factorization many things. Sometimes we wrongly assert that integer factorization is prime decomposition (which is the base of the fundamental theorem of arithmetic); nonetheless, we could also assume that integer factorization is to identify all the positive factors that divide a numberevenly. It's important for us to learn the differences between these two concepts since they are not the same. And obviously their implementation in code is also very different.
Let us take the number 28 for example.
The prime decomposition of 28 can be expressed as:
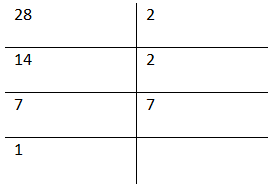
∴ 28 = 2² x 7
In the other hand the divisors of 28 are: 1, 2, 4, 7, 14, 28.
As you can see from the comparison above, some of the divisors can also be expressed as prime products. The problem statement requires counting the divisors instead of the prime factors, but we could use both definitions to get the same result.
I will talk about divisors and a shortcut to counting them before going into prime decomposition; primes are a world apart and need special attention.
Exact Division
The definition of the arithmetic division states that the dividend must be expressed by the product of the divisor and the result of the actual division.
For example:
28 ÷ 4 = 7 ∴ 7 x 4 = 28
This special property allows us to use a shortcut to calculate the positive factors of an integer. The basic idea is that if we double the amount of positive factors of the integer square root approximation of the number, we will find the actual amount of factors.
If we modify our code with that observation in mind we can see a ridiculous performance boost when comparing the results with the previous implementation.
for( int i = 1; true; ++i )
{
// Obtaining the triangle number
//
int triangle = i * ( i + 1 ) / 2;
int factors = 0;
// Counting the factors
//
for( int k = 1; k <= sqrt( triangle ); ++k )
{
if( triangle % k == 0 ) ++factors;
}
factors *= 2;
// If factors are bigger than 499 then exit
//
if( factors > 499 )
{
std::cout << "Triangle number: " << triangle << " factors: " << factors << std::endl;
break;
}
}
Results
Triangle number: 76576500
Time: 0.224segs
As you can see, the time of execution has been reduced to a fifth of a second. The performance bump can be attributed to the reduction of checks we do to find factors, since now our loop goes from one to the square root approximation of our triangle number and not the number itself.
This improvement got us the solution of the problem in a very fast manner, but bear in mind that this will not work if our triangle number is a perfect square.
Primes to the rescue
By using prime decomposition we can make our code work for any scenario, perfect squares included. This last optimization will improve the performance of our code in terms of time and will reduce the edge cases to virtually none.
Let us revisit the prime decomposition of the number 28:
28 = 2² x 7
Now let us count the positive divisors (factors) of 28: 1, 2, 4, 7, 14, 28.
Grouping the exponents of the prime decomposition of 28 we end up with 2, 1, the theory states that if we add 1 to each exponent and then multiply them together we will get the total of positive divisors of 28.
28 = 2² x 7
(2 + 1), (1 + 1) = ( 3, 2 ) → 3 x 2 = 6
As you can see we have successfully used prime decomposition to retrieve the amount of factors of 28.
Our new "trick" creates a new problem, we need to do the prime decomposition, which implies that we need to implement an algorithm to find primes. Finding primes is not an easy task but implementing an effective algorithm to find them is very important.
Prime Sieves
Prime numbers and their relevance have been a fascinating subject of study to many mathematicians over time.
Due to their special property of only being divisible by themselves and the unity, finding primes using brute force can be very instruction intensive for our CPU. Just imagine that if we brute force our way to find if 13 is a prime number we have to try at least 11 residue checks; the amount of checks increases linearly for higher numbers.
In order to tackle this issue there are some old algorithms that help us find primes up to a number called prime sieves. According to, Wolfram Alpha, a sieve is a process of successively crossing out members of a list according to a set of rules such that only some remain.A prime sieve works by creating a list of all integers up to a desired limit and progressively removing composite numbers (which it directly generates) until only primes are left.
The sieve of Eratosthenes is one of the best known prime sieves. It's also considered to be one of the simplest to implement in code.

The previous image illustrates how the sieve of Eratosthenes works. The sieve of Eratosthenes along with other factorization techniques, like wheel factorization, reigned the prime decomposition scene up until 2003 when the paper PRIME SIEVES USING BINARY QUADRATIC FORMS by A. O. L. ATKIN AND D. J. BERNSTEIN introduced a faster (but more complicated) sieve to find prime numbers: the sieve of Atkin.
For this example we will use the translation into C++ of the pseudo-code described in the paper.
const int max_n = 300;
std::vector primes;
bool sieve[max_n];
void sieveOfAtkin(){
int N = sqrt(max_n);
memset(sieve, 0, sizeof(sieve));
for (int x = 1; x <= N; x++){
for (int y = 1; y <= N; y++){
int n = (4*x*x)+(y*y);
if (n <= max_n && (n % 12 == 1 || n % 12 == 5))
sieve[n] ^= true;
n = (3*x*x)+(y*y);
if (n <= max_n && n % 12 == 7)
sieve[n] ^= true;
n = (3*x*x)-(y*y);
if (x > y && n <= max_n && n % 12 == 11)
sieve[n] ^= true;
}
}
sieve[2] = sieve[3] = true;
primes.push_back(2);
primes.push_back(3);
int a;
for (a = 5; a <= N; a+=2){
if (sieve[a]){
for (int i = a*a; i < max_n; i += a*a)
sieve[i] = false;
primes.push_back(a);
}
}
for (; a < max_n; a+=2) if (sieve[a])
primes.push_back(a);
}
Following the sieve definition and the flow described in the illustration above this code retrieves all the prime numbers under 300, which is all we need to complete our last optimization of our solution.
The basic idea is to do a "warm up routine" where we store in a container all the prime numbers we are going to use for the residue check of our triangle number. Then we are going to do the prime decomposition and implement our trick to calculate the amount of positive divisors from the exponents of our prime factors.
Our counting implementation looks like this:
int countFactors(int n)
{
int initial_n = n;
int factors = 1;
for (int i = 0; primes[i] * primes[i] <= n; ++i)
{
int power = 0;
while (initial_n % primes[i] == 0)
{
initial_n /= primes[i];
++power;
}
factors *= power + 1;
}
if (initial_n > 1)
{
factors *= 2;
}
return factors;
}
And our resulting program looks like this:
// Warm up - retrieving all primes under 300 sieveOfAtkin();
//
for( int i = 1; true; ++i )
{
// Obtaining the triangle number
//
int triangle = i * ( i + 1 ) / 2;
// Counting the factors
//
int factors = countFactors(triangle);
// If factors are bigger than 499 then exit
//
if( factors > 499 )
{
std::cout << "Triangle number: " << triangle << " factors: " << factors << std::endl;
break;
}
}
Results:
Triangle number: 76576500
Time: 0.004segs
Conclusion
The goal of this exercise was to demonstrate the importance of iterations in software development. We started with a simple ineffective solution and iterated over it until we got something we were more comfortable with in terms of readability and performance.
More importantly, knowing how to find prime numbers and how to implement prime factor decomposition is crucial for programmers. Prime numbers are strongly tied to cryptography and other areas of in the computer industry.
The mathematicians who studied prime numbers hundreds of years ago used the knowledge from primes to develop new areas of mathematics, like number theory and knot theory, which are widely used today in programming.
While you might not use prime numbers directly yourself, they are a key part of modern mathematics and have important uses in the era of computers.